Falls Du es verpasst hast: Am 28. September hatten wir auf Facebook ein Rätsel veröffentlicht, bei dem es darum ging, die fehlende Teilfläche eines Quadrats zu bestimmen.

Hier nochmal die Aufgabe

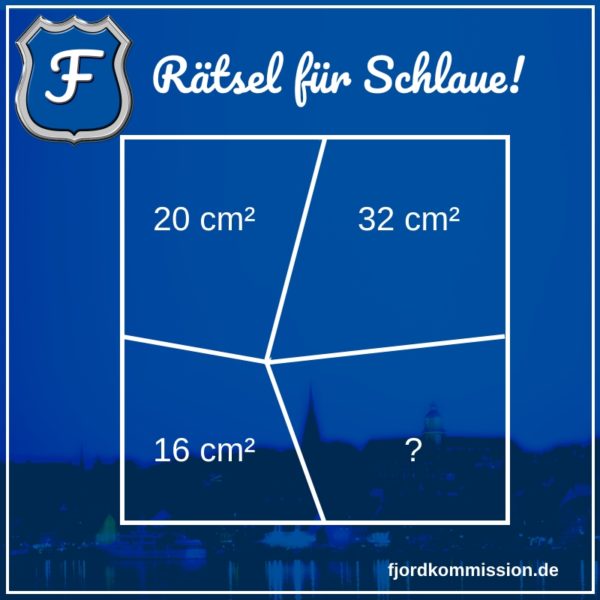In dem Quadrat wurde ein Punkt beliebig in die Fläche gesetzt. Von diesem Punkt aus führen Linien zur Mitte der jeweiligen Seite des Quadrats.

Drei der entstandenen Flächen sind bekannt, wie in dem Bild angegeben.

Wie groß ist die vierte Fläche?

Hinweis: Das Quadrat ist nur eine Skizze und nicht maßstabsgerecht gezeichnet. Messen nützt also nichts. 🙂

Noch ein Hinweis: Mit Methoden aus der Mathematik des 7. Schuljahres lösbar.

Hier nun die Auflösung

Es gibt mehrere Lösungsansätze, die zum Ziel führen.

Der einfache (intuitive) Weg

Im Quadrat sind die Summen der einander gegenüberliegenden Teilflächen gleich groß (muss man wissen oder „im Gefühl haben“). Das heißt, die Flächen links unten und rechts oben sind zusammen genauso groß wie „links oben“ plus „rechts unten“.

Damit ergibt sich

16 cm² + 32 cm² = 20 cm² + ?

Also ist „?“ = 16 cm² + 32 cm² – 20 cm² = 28 cm²

Der Weg über die Dreiecke

Wem der intuitive Weg nicht Beweis genug ist, da die Annahme nötig ist, dass die gegenüberliegenden Flächen zusammen jeweils gleich groß sind, geht etwas mathematischer vor.

Als Hilfslinien zeichnen wir uns darum Verbindungen vom Punkt in der Fläche zu den Ecken des Quadrats und erhalten dann insgesamt acht Teilflächen.

Da wir aus der Mathematik der 7. Klasse wissen, dass die Fläche eines Dreiecks gleich (Grundseite * Höhe) / 2 ist, können wir folgern, dass die beiden Dreiecke über den jeweiligen Seiten des Quadrats gleich groß sein müssen. Denn ihre Grundseite ist jeweils die Hälfte einer Quadratseite, und die Höhe ist ebenfalls immer gleich dem Abstand von der Seite zu unserem willkürlichen Punkt in dem Quadrat. Der Punkt muss dafür nicht in der Mitte liegen. Die beiden Dreiecke nebeneinander sind dennoch gleich groß.

Damit können wir die Dreiecke, die gleich groß sind, mit den Namen a, b, c und d versehen.

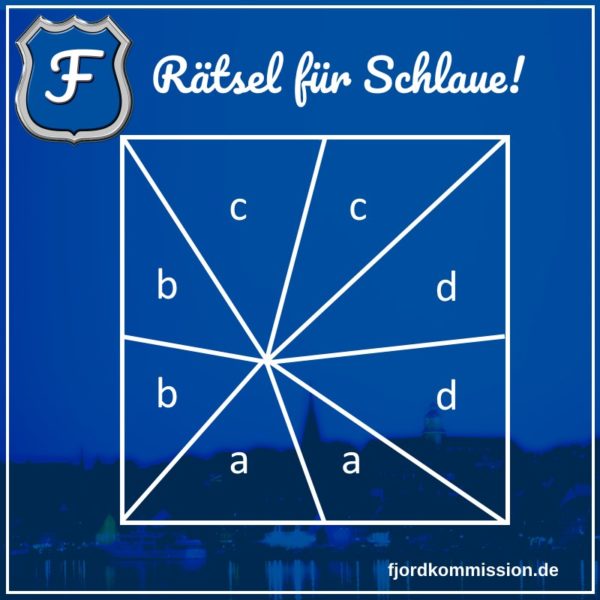
Die beiden Dreiecke a + b unten links sind ja unsere Fläche mit 16 cm². Darüber, oben links, sind b + c = 20 cm², und oben rechts haben wir c + d mit 32 cm². Bleibt als gesuchte Fläche „a + d“ = ?.

Wenn wir das Bild jetzt genauer betrachten, sehen wir, dass die Fläche unten links a und b enthält, und die Fläche oben rechts c und d. Die beiden haben zusammen also je ein Dreieck von a, b, c und d.

Dasselbe gilt für die anderen beiden Flächen: oben links b und c und unten rechts a und d. Also auch diese beiden bestehen aus je einem Dreieck a, b, c und d.

Daraus folgt, dass die beiden Flächen zusammen jeweils gleich groß sein müssen, da die a’s, b’s, c’s und d’s ja jeweils gleich groß sind.

Das heißt:

(a + b) + (c + d) = (b + c) + (a + d)

Was sich ja allein schon daraus ergibt, dass auf beiden Seiten des Gleichheitszeichens dieselben Buchstaben, nur in verschiedener Reihenfolge vorkommen.

Die bekannten Werte eingesetzt erhalten wir

16 + 32 = 20 + (a + d)

Damit ist dann (a + d) wie oben wieder:

16 + 32 - 20 = 28

Der umständliche Weg über ein Gleichungssystem

Wem die Akzeptanz des Satzes nicht ausreicht, dass die gegenüberliegenden Seiten zusammengenommen gleich groß sind, kann auch das ganze über ein Gleichungssystem herleiten.

Notieren wir uns zuerst, was wir wissen.

a	+	b					=	16
		b	+	c			=	20
				c	+	d	=	32
a	+					d	=	x

Füllen wir nun die leeren Plätze mit Nullen auf, um ein Gleichungssystem zu erhalten:

a	+	b	+	0	+	0	=	16
0	+	b	+	c	+	0	=	20
0	+	0	+	c	+	d	=	32
a	+	0	+	0	+	d	=	x

Wenn wir alle Spalten untereinander addieren, erhalten wir die Gleichung

(a + 0 + 0 + a) + (b + b + 0 + 0) + (0 + c + c + 0) + (0 + 0 + d + d) = 16 + 20 + 32 + x

Oder einfacher:

2a + 2b + 2c + 2d = 68 + x

Umgeformt:

2(a + b + c + d) = 68 + x

Teilen wir beide Seiten durch 2, erhalten wir

a + b + c + d = 34 + x/2

Ersetzen wir wieder a + b und c + d durch die bekannten Zahlen, ergibt sich

16 + 32 = 34 + x/2

Ziehen wir nun auf beiden Seiten 34 ab und nehmen das mal 2

(16 + 32 - 34) * 2 = x
(48 - 34) * 2 = x
14 * 2 = x

x ist also, welche Überraschung, auch hier 28.